밍경송의 E.B
[사이버보안] 암호개념, 대칭암호화 본문
이 글은 2024-1 ㅇ화여대 사이버보안개론 수업자료를 참고하였음을 밝힙니다.
🔑암호(Cryptography)
: 중요 정보를 다른 사람들이 해석할 수 없게 하는 방법 (!=PW)
- 암호 작성술: 체계 디자인
- 암호 해독 : 해독,체계 분석
- 암호학 :암호 연구 등 포괄
- 평문과 암호문
- 암호화 알고리즘 : 평문 -> 암호문으로 변경
- 암호화 키(Encryption key)
: 암호화/복호화 시 양쪽이 알고 있어야 하는 수단
** 암호화 알고리즘은 반복 사용 . 키는 지속적으로 변경해서 사용 **
암호화 과정

복호화 과정

[암호기법의 분류]
| 치환(substitution) 암호 : 비트, 문자, 블록을 다른 "로 대체 |
전치 암호(transposition) : " 이 원래 의미를 감추도록 재배열 |
| 블록 암호 : 특정 비트 수의 집합을 한 번에 처리 | 스트림 암호 : 데이터 스트림을 순차적으로 처리 |
[관련 주요 기술]
- 대칭.비대칭 암호(뒤에서 다룸)
- 일방향 해시함수 (복호화 안함. 무결성 보장. 암호화상태로 저장)
- 메시지 인증코드 : 전송도중 메세지가 변경 X것과, 원래의 통신 상대로부터 왔음을 확인 (무결성, 인증)
- 전자서명 : 무결성확인, 인증과 부인방지
- 의사난수생성기 -> 키생성 역할
좋은 암호 sys는 암/복호화는 쉽고 빠르고, 해독은 어려운 sys다!
[역사]
1) 스키테일 암호 - 전치법 사용(재배열)

2) 시저 암호 - 알파벳 한 글자를 다른 한 글자로 대체 (단일치환)
* 키 : 원 알파벳으로부터 몇 칸 이동할지
* 전사공격에 취약

3) 단일치환 암호 - 26글자의 알파벳을 각각 다른 알파벳에 대응 (알고리즘 개선)
* 복호화를 위해 매칭표 필요
* 빈도 분석법에 취약

4) 다중치환 암호 - 한 글자가 암호화 키와의 매핑 => 여러 글자로 대체됨 (!= 단일 치환)
ex 비즈네르 암호 -> 빈도분석법에 다소 강함

🗝️ 대칭키 암호화 방식 🗝️
암호화 키 = 복호화 키
걸리는 시간 짧고, 비교적 단순
[KEY]
- 길이가 길수록, 전사공격에 강함
- 키는 평문과 같은 가치를 지님 ( if 키 open? => 평문도 open..)
- 종류
- 재사용여부)
- 세션키 : 통신 때마다 한 번 사용 (SSL/TLS 암호화통신)
- 마스터키 : 반복 사용
- 암호화대상)
- CEK(Contents)
- KEK(Key) - 키를 암호화하기 위한 키
- 재사용여부)
대칭 암호화 알고리즘
[1 DES]

- 1997년 미국 연.정.처의 표준암호로 채택
- 64bit 평문 -> 64bit 암호문으로
- 64bit 블록 암호화 알고리즘
- key 크기 : 56bits
- 전사 공격으로 해독 가능 -> 사용 중단
*과정
1) Pre - Processing : 초기 permutation 실행
- 입력 : 64bit 평문 조각 -> bit 위치를 규칙에 의해 바꿈
- L과 R로 32bit씩 나눔
2) 16번의 중간 라운드 수행
- 입력 : 이전 라운드의 L과 R

*L의 경우 이전 R이 그대로 들어감.
**R의 경우 이전 R과 그 단계의 subkey를 f 한 후 이전 L과 XOR 연산 진행(같: 0, 다: 1)

3) Post - Processng : 최종 permutation 실행
- 입력 : 이전 L과 R
- L과 R을 하나의 블록으로 만듦
- 초기전치(1단계)의 역전치 적용

[2 Triple DES]
- DES의 대안으로 DES를 연속 3번 실행하는 방식
- 암호화 -> 복호화 -> 암호화
- 목적에 따라 사용하는 키의 개수가 달라짐
- 모든 키를 동일하게 하는 경우 - 기존 DES와 호환성 유지
- 2개의 키 (같은 키로 암호화-> 복호화 : 중간에 그냥 평문이 나옴)
- 3개의 키 - 암호화를 2번하는 효과
- DES보다 2배 강도가 강함
[3 AES]
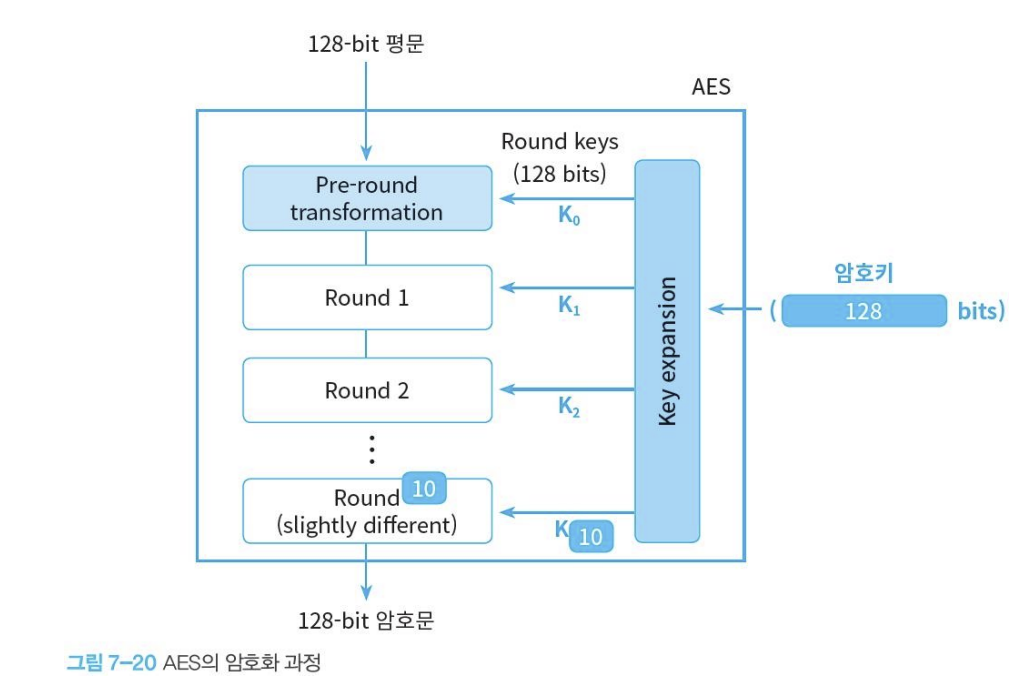
- 1997년 암호공모에서 채택
- 128bit 평문을 128bit 암호문으로
- key의 크기 : 128, 192, 256 bit
- 라운드 회수: 10,12,14
*과정
1) SubBytes : byte단위로 substitution 수행
2) ShiftRows : row 단위로 cyclic shift 수행 (permutation)
3) MixColumns : 높은 diffusion을 위해 column 단위로 mix
4) AddRoundkey(마지막연산) : roundkey와 state XOR

[SEED]
- 국산 128bit 블록 암호 알고리즘, 전자상거래 등의 중요정보 보호 목적
[ARIA]
- 국산 128bit 블록 암호 알고리즘, 경량 환경 HW 효율성 향상
[IDEA]
- 유럽에서 많이 사용. 64 bit -> 64bit로 . 128 bit key, 8라운드
- 16bit 단위로 연산이 이루어짐, 주로 키 교환에 쓰임
[RC5]
- 미국 RSA 연구소에서.
- 입출력, 키, 라운드 수가 가변인 블록 알고리즘
- DES 속도의 10배
[Skipjack]
- 64bit 입출력. 80bit 키 32라운드. 칩에 내장
[LEA]
- 국내 개발. 경량환경
- 128bit 데이터 블록. 비밀 키 사용가능
| 블록 암호 | - 특정 비트 수의 집합을 한 번에 처리 8bit 혹은 16bit에 비례 -> 라운드 사용. 반복적 암호화 과정 수행 - 일반 데이터 전송, 저장 |
| 스트림 암호 | - 한 번에 1bit나 1byte의 data stream을 순차적으로 처리 plain text와 key를 bit마다 XOR - 군사. 외교용으로 주로 사용 |
🔒블록암호
: 평문을 블록단위로 나누어서 암.복호화 수행
** 블록 단위로 나누고 남은 짜투리 부분도 블록단위에 맞추기 위해 패딩 추가
[블록암호모드]
1 ECB 모드
- 각 평문 블록을 암호화한 것이 그대로 암호문 블록이 되는 방식
- 장 : 계산 단순, 블록 간 독립(한 블록 오류-> 다른 블록에 영향 안 줌), 병렬처리 가능
- 단 : 보안적으로 취약
- 중간 블록 바꿔치기해도 이상 없음
- 같은 plain text -> 같은 cipher text : 단서 제공

2 CBC 모드
- 암호문 블록을 체인으로 연결
- 현재의 평문 블록 XOR 직전의 암호블록 -> 암호화
- 초기화 벡터 : 최초 블록 암호화할 때 XOR에 사용되는 블록으로 송수신자가 알고 있어야 함.
- 장 : 안전. 변조 불가
- 단 : 병렬처리 불가. 복잡.. 중간에 있는 블록만 복호화 못함.

[현대 블록 암호]
1) Substitution (S-box)
- 혼돈 제공.
- 평문과 암호문의 상관관계 감추기. 평문 내용 짐작이 어렵게 함.
2) Permutation (P-box)
- 확산 제공
- 평문의 통계정 특성을 암호문 전반에 확산.패턴 추론이 어렵게 함.
3) XOR
[블록암호구조]
| Feistel | - 구조 : 암호화 방식이 특정 계산 함수의 반복으로 구성(라운드 함수) ex DES, SEED - 강도를 결정짓는 요소 : 평문 블록 길이, 키 길이, 라운드 수 - 안정성 조건 : 평문 64bit 이상, 키 128 권장, 라운드 16회 이상 - 특성 : 복호화 과정 = 암호화 과정 -> 복호화 과정의 input : 암호문, 보조키 입력 순서는 암호화 과정과 반대 |
| SPN | - 구조 : Substitution과 Permutation의 중첩 -> input을 블록으로 나눔 -> 각 블록을 S-> 출력을 P 반복 ex AES, IDEA, ARIA - 특성 : 암호화 함수 != 복호화 함수 => 복호화를 위해 라운드 함수 역변환 필요 - HW구현이 용이 but 비용높음 |
'CSE > 사이버보안개론' 카테고리의 다른 글
| [사이버보안] 블록체인 (1) | 2024.06.09 |
|---|---|
| [사이버보안] 암호기반 인증- Hash, MAC, 전자서명, 공개키 기반 구조 (1) | 2024.06.07 |
| [사이버보안] WEB (0) | 2024.04.25 |
| [사이버보안] 네트워크보안 - Sniffing, Spoofing, Session hijacking (0) | 2024.04.24 |
| [사이버보안] 네트워크 보안 - DoS, DDoS, DRDoS, Network Scanning (0) | 2024.04.24 |




