밍경송의 E.B
<2> 순환(Recursion) 과 반복(Iterative) 본문
이 글은 시험이 2일하고 18시간정도 남은 사람이 내용 정리를 위해 적는 글입니다.
*[C언어로 쉽게 풀어쓴 자료구조] 책과 숙영리 교수님의 강의를 참고하여 작성하였음을 밝힙니다.
🤔시작 전 정리사항
분할 정복(Divide Conquer) 과 동적 프로그래밍(Dynamic programming)
1) 분할 정복
: 주어진 문제를 더 작은 동일한 문제들로 분해하여 해결하는 방법
*특징
- Recursive(순환) method
- 각 Sub-problem들은 독립적으로 해결됨.
- Top-down 방식
2) 동적 프로그래밍
: 큰 문제를 작은 문제로 나누어 풀어 해결하는 방법
*특징
- Iterative (반복) method
- 각 Sub-problem들은 종속적임.
- Bottom-up 방식
@ 1)과 2)의 명확한 차이
: Sub-problem들에서 중복(반복)이 일어나는지 안일어나는지를 확인!
🤔 분할 정복은 큰 문제를 해결하기 어려워 단지 작은 문제로 나누어 푸는 방법. 작은 문제에서 반복이 일어나는 부분이 없다는 점.
-> 문제의 크기가 순환이 진행될 수록 작아짐.
🤔 동적프로그래밍은 작은 부분 문제들이 반복되는 것을 이용해 풀어나가는 방법. Sub-problem들의 답이 항상 같아야 함.
(출처:https://galid1.tistory.com/507)
🃏 팩토리얼 프로그래밍
1) 순환을 이용한 방법 (Recursive) O(N)
- 정의
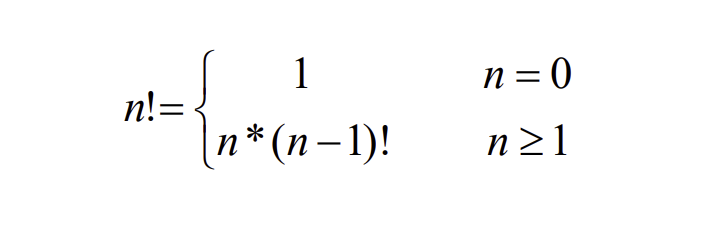
- 코드
int factorial(int n)
{
if(n<=1) return(1);
else return ( n*factorial(n-1) );
}
- 이해
: factorial(3) = 3 * factorial(2) = 3 * 2 * factorial(1) = 3 * 2 * 1
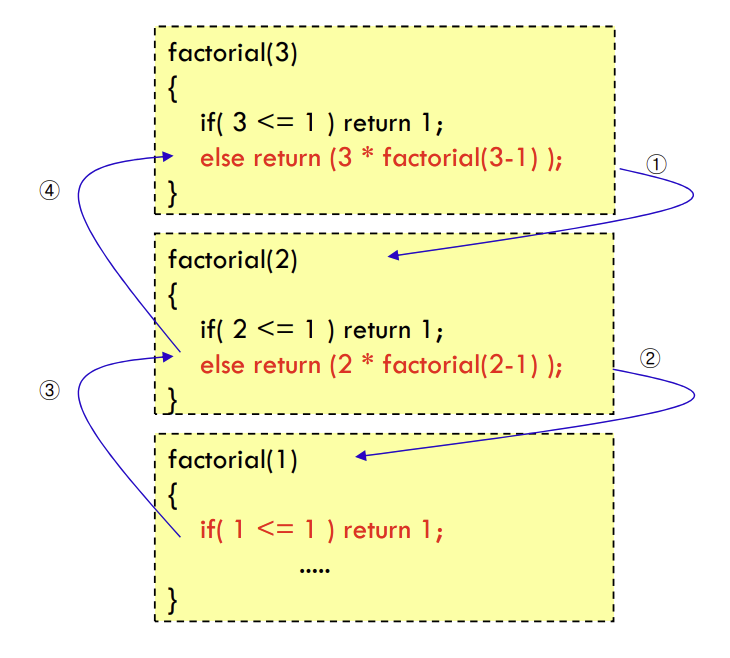
🤔 활성 레코드 (Activation record) (=stack frame)
: Context switching을 하기 전에 함수 상태를 기록하고 복원하기 위해 정보를 담아두는 runtime structure
*정보에 포함되는 것
- 지역 변수 (local variable)
- 반환 주소 (return address)
- 값 파라미터 (input parameter)
- 반환 값 (return value)
" 함수가 호출될 때 스택에 push되고, 컨트롤이 caller 함수(원함수)로 돌아갈 때 스택에서 pop된다"
=> 순환 호출이 계속 중첩될 수록 시스템 스택에는 활성레코드들이 쌓임.
"Recursive algorithm의 time complexity는 몇번의 호출 (= system stack에 몇번의 push-and-pop)이 있었는가로 결정된다." 스택에 몇 번 들어갔다 왔니..?
🤔 순환 알고리즘의 구조
1) 순환을 멈추는 부분 ** 만약 이 부분이 없다면 시스템 오류가 발생할 때까지 무한정 호출
ex) 팩토리얼 예제 if ( n <= 1 ) return 1
2) 순환 호출을 하는 부분
ex) 팩토리얼 예제 n* factorial(n-1)
2) 반복을 이용한 방법 (Iterative) O(N)
-정의
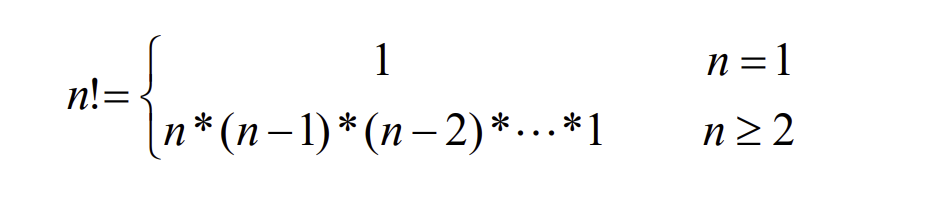
-코드
int factorial_iter(int n)
{
int k, v=1;
for (k=n, k>0; k--)
v=v*k;
return(v);
}
순환 <-> 반복
: 순환 호출이 끝에서 이루어지는 순환 (꼬리 순환)의 경우 반복 알고리즘으로 쉽게 바꾸어 쓸 수 있음.
✔️다시 한 번 정리
순환
: 문제의 일부를 해결한 다음, 나머지 문제에 대하여 순환 호출을 함.
(호출/수행 될 때마다 해결된 부분과 남아있는 부분이 존재함)
==> 해결되는 부분이 매 호출마다 존재하기 때문에 호출할 수록 문제의 크기는 작아짐 !
🤔 when?
=> 알고리즘의 정의가 순환적으로 되어있는 경우에 유리 (..멩?)
ex) 팩토리얼 함수, 피보나치 수열, 이항계수 계산, 이진트리 알고리즘, 이진 탐색, 하노이 탑 문제 등
🤔 성능?
위에서 언급했듯, 순환과 반복의 방법 모두 팩토리얼 계산의 경우 O(n)으로 동일.
but, 순환 호출 시 호출이 일어날 때마다 호출하는 함수의 상태를 기억해야 하므로 여분의 기억장소가 필요하다는 단점 O
=> 팩토리얼 계산의 경우 반복적인 방법이 속도가 더 빠르다!
🃏 거듭제곱 값 ( X^n ) 계산하기
1) 반복을 이용한 방법 (Iterative) 1 O(N)
-코드
double slow_power(double x, int n)
{
int i;
double result = 1.0;
for (i=0; i<n; i++)
result=result*x;
return(result);
}: for문을 N번 돌기 때문에 O(n)!
2) 순환을 이용한 방법 (Iterative) O(log N)
-알고리즘
power(x, n) :
if n==0
then return 1;
else if n이 짝수
then return power(x^2, n/2);
else if n이 홀수
then return power(x^2, (n-1)/2);
: x^n = (x^2)^n/2 를 이용하여 n이 짝수인 경우에는 x^2를 먼저 -> 후에 n/2제곱 | 홀수인 경우에는 x^2를 (n-1)/2 제곱 -> x 곱하기
-코드
double power(double x, int n)
{
if(n==0) return 1;
else if ( (n%2 ==0) )
return power(x*x, n/2)
else return x*power(x*x, (n-1)/2);
}
-예시 (으에엑 수포자는 어려워..)
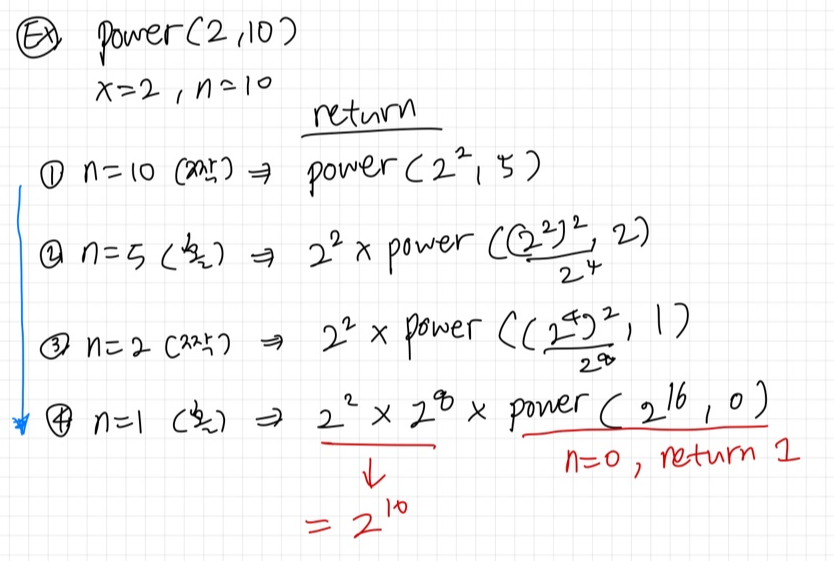
🤔: 순환적인 방법이라서 단계를 거듭할 수록 문제의 크기가 줄어들고 있음을 확인할 수 있다!
: 몇 번의 순환호출이 일어나는가?
= 몇 번의 Activation call이 발생하는가?
= 시간복잡도가 어떻게 나타나는가?
= k번 순환호출 => n=2^k => k= log n
🤔 매 호출마다 n은 (최소한) 절반으로 줄어들게 되고, 이것은 로그 시간 복잡도를 나타낸다 끼약
3) 반복을 이용한 방법 (Recursive) 2 O(log N)

- 예시
[input : n=29 --> output : x^29]
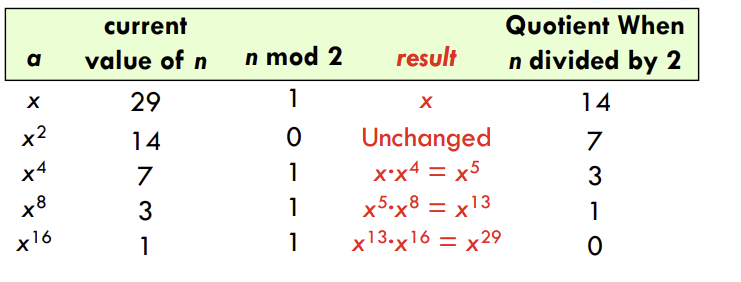
: n-> n/2 -> n/2/2 -> ... 0 => O(log n)
🃏 피보나치 수열
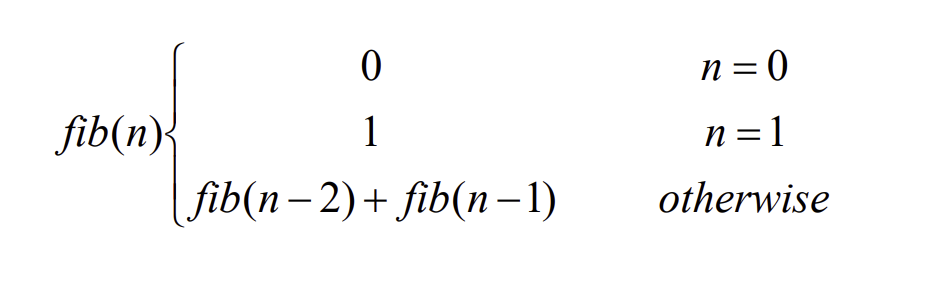
1) 순환을 이용한 방법 (Iterative) O(2^n)
-코드
int fib(int n) {
if(n==0) return 0;
if(n==1) return 1;
return (fib(n-1) + fib(n-2));
}
🤔 순환 호출을 사용했을 때의 비효율성
: 같은 항이 중복해서 계산됨
ex) fib(6)을 호출하는 경우, fib(3)이 4번이나 중복 계산됨. ==> n이 커지면 더욱 심해짐 !
*why?
: 중간에 계산되었던 값을 기억하지 않고 다시 계산하기 때문!
2) 반복을 이용한 방법 (Iterative) O(N)
-코드
int fib_iter(int n)
{
if(n==0) return 0;
if(n==1) return 1;
int pp = 0;
int p = 1;
int result =0;
for(int i=2; i<=n; i++) {
result =p + pp;
pp=p;
p=result;
}
return result;
}
-정리
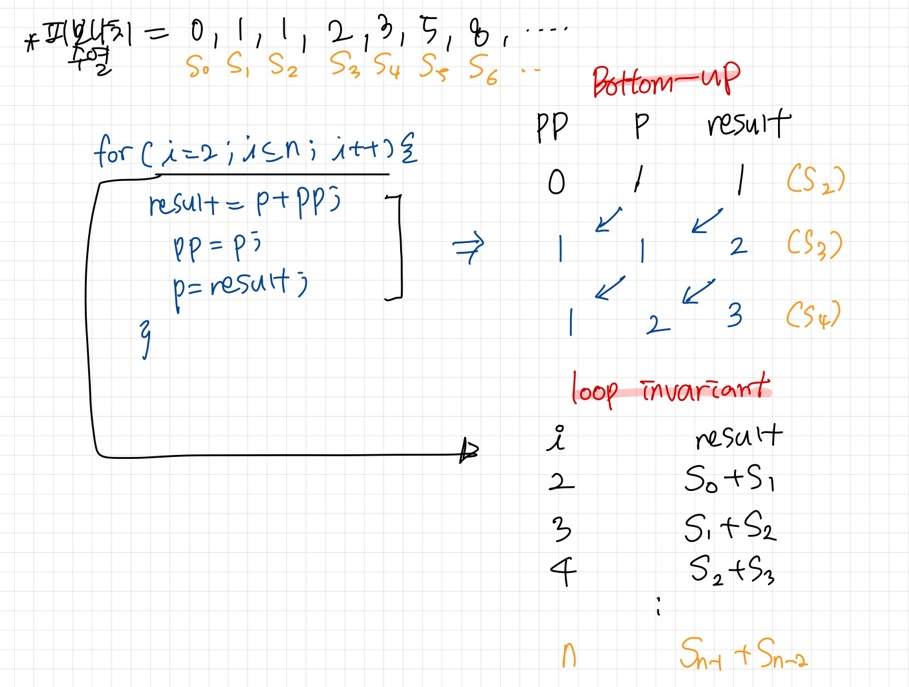
: loop invariant의 경우, i에 따라 도출되는 result의 규칙이 모두 같다는 의미
🤔 피보나치 수열의 경우 반복적인 구조를 이용하면 더 나은 결과를 얻을 수 있음 !
🃏 하노이탑 문제
: 막대 A에 쌓여있는 원판 n개를 막대 C로 옮겨라 !
*조건
- 한 번에 하나의 원판만 이동할 수 있음.
- 맨 위에 있는 원판만 이동할 수 있음.
- 크기가 작은 원판 위에 큰 원판이 쌓일 수 없음.
- 중간의 막대를 앞의 조건들을 지켜서, 임시적으로 이용할 수 있음.
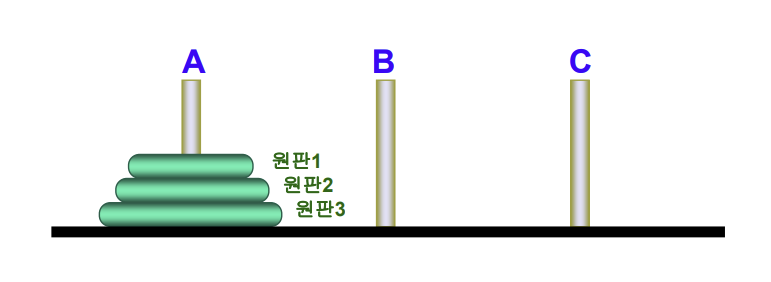
: 문제의 크기 = 이동해야 하는 디스크의 개수
🤔How?
: n개의 원판이 A에 쌓여있는 경우
1) 먼저 n-1개의 원판을 B로 옮긴 후, 제일 밑 원판(크기가 제일 큰)을 C로 옮김
2) B에 있던 n-1개의 원판을 C로 옮김
-알고리즘 (A : from, B : tmp, C: to)
void hanoi_tower( int n, char from, char tmp, char to) {
if (n==1) {
from에 있는 한 개의 원판을 to로 옮긴다.
}
else {
1) from에 맨 밑의 원파을 제외한 나머지 원판들을 tmp로 옮긴다.
2) from에 있는 한 개의 원판을 to로 옮긴다.
3) tmp의 원판을 to로 옮긴다.
}
: 1) 과 3)의 경우 원래 문제의 축소된 형태임 --> 문제의 크기가 n대신 n-1로 축소
=> 함수의 매개변수를 n-1로 바꾸어 순환호출하면 됨.

🤔순서 주의 ! from -> tmp 후에 tmp -> to
✔️순환의 파워를 가장 극명하게 보여주는 하노이탑 문제 !!! 끝
—
🃏 Tail recursion VS Head recursion
- Tail recursion : 꼬리 순환은 순환 호출이 순환 함수의 맨 끝에서 이루어지는 형태의 순환
=> 반복적인 형태로 변환이 쉽다
Ex) return n * factorial(n-1);
- Head recursion : 머리 순환은 순환 호출이 순환 함수의 맨 앞에서 이루어지는 형태의 순환
+ Multi recursion : 하노이탑 문제와 같이 여러 군데에서 자기 자신을 호출하는 경우
=> 반복적인 형태로 변환이 어렵다
Ex) return factorial(n-1) * n;
'CSE > 자료구조&알고리즘' 카테고리의 다른 글
| <4> 스택(Stack) (0) | 2023.10.26 |
|---|---|
| <3> 배열, 구조체, 포인터 (0) | 2023.10.25 |
| <1> 자료구조와 알고리즘 (0) | 2023.10.24 |
| 선택 정렬(Selection sort)와 삽입 정렬(Insertion sort) (1) | 2023.04.22 |
| 빅 오 표기법 - O(1), O(N), O(log N) (0) | 2023.04.17 |




