밍경송의 E.B
<3> 배열, 구조체, 포인터 본문
이 글은 시험이 2일하고 18시간정도 남은 사람이 내용 정리를 위해 적는 글입니다.
*[C언어로 쉽게 풀어쓴 자료구조] 책과 숙영리 교수님의 강의를 참고하여 작성하였음을 밝힙니다.
🃏배열
: 같은 형의 변수를 여러 개 만드는 경우에 사용하는 자료 구조

🤔연속적인 메모리 공간이 할당되고 인덱스 번호를 이용하여 쉽게 접근이 가능함(readability ↑)
- random access lookup time = O(1)
- add new element at Kth index = O(N)
🤔0부터 N까지의 ID가 할당되는 데이터를 처리하기 위해서는 (N+1) element 크기의 배열이 필요함
-> 인덱스는 0부터!
*예시
double A[10]; <= 80byte의 연속된 메모리 블럭이 할당됨.
: A[i] : i = 시작번지로부터의 (sizeof(double) 크기 만큼의) offset
ex) A[4] = A[0] + 4*sizeof(double) = base + 4*sizeof(double)
🤔자료형 크기 간단 정리
- Bool, char : 1B
- Short : 2B
- int, float : 4B
- double : 8B
- long : 4B(32 OS) / 8B(64 OS)
- pointer : 4B(32 OS) / 8B(64 OS)


🃏 구조체
: 타입이 다른 데이터를 하나로 묶는 방법

- sturct 구조체이름 구조체변수; <- 위의 예제에서는 생략됐으나 위 과정이 있어야 구조체 생성됨.
- 구조체 안에 들어있는 멤버를 사용하려면 '.' <- 멤버 연산자 이용
- typedef를이용해 구조체를 새로운 타입으로 선언 가능 / 위의 예제에서 구조체의 이름은 student
🃏 배열의 응용 : 다항식
Q: 두 다항식의 덧셈을 해야한다고 가정할 때 아래의 질문을 고민해보자!
- coefficient(계수)와 exponent(차수)를 컴퓨터에 어떻게 표현할까?
- N차 다항식에서 n= exponen가 가장 큰 값일 때, n을 기억하는 것이 필요할까?
- coefficient가 0인 항과 아닌 항을 구별하는 것이 좋을까?
- 차수는 높은데, 항의 개수가 적은 (ex. x^100 + 10) 다항식은 어떻게 표현하는 것이 공간/시간적으로 효율적일까?
1) 배열을 이용한 첫번째 방법
: 모든 차수의 계수(coef)값을 배열에 저장하는 것. 하나의 다항식 = 하나의 배열

🤔장점
: 다항식의 덧셈, 뺄셈 연산 알고리즘이 간단함.
🤔단점
: 희소다항식( 대부분의 항의 계수가 0인 경우)을 표현할 때 공간 낭비가 심함.
*덧셈 프로그램

: 구조체 A, B의 coef 배열을 스캔하면서 차수가 큰 항을 구조체 C로 이동함.
if 차수가 같으면 구조체 A,B의 coef 값을 더하여 C의 coef에 대입함.
2) 배열을 이용한 두번째 방법
: 다항식에서 0이 아닌 항만을 배열에 저장하는 것. (계수, 차수) 형식으로 배열에 저장

🤔장점
: terms의 항의 총 개수가 MAX_TERMS만 넘지 않으면 많은 다항식을 저장 가능함.
🤔단점
: 인덱스 변수 관리 + 차수 저장으로 인해 더 많은 공간이 필요함 + 첫번째 방법보다 연산이 어려움.
* avail 변수 : 현재 비어있는 요소의 인덱스를 가리킴 = 현재 available한 가장 작은 값을 가진 index를 가리킴.
*덧셈 프로그램


: attach() = 해당 항목을 배열의 다음 빈 공간에 더하는 함수. 이때 avail 변수가 증가됨에 유의!
-> 순서대로 A와 B의 각 항의 차수를 비교하여, 차수가 같으면 A와 B 각 항의 계수를 더하여 C로 옮기고 차수가 다르면 A와 B 중 큰 항을 C로 옮김.
* 어느 한쪽 다항식이 끝나게 되면 A나 B 중 남아있는 항목들을 전부 옮기면 됨.

🃏 희소행렬 (Sparse Matrix)
*배열을 이용하여 행렬을 표현하는 방법은 다항식을 표현하는 방법과 유사함.
1) 2차원 배열을 이용하여 배열의 전체 요소를 저장하는 방법
장점: 행렬의 연산을 간단하게 구현 가능
단점: 대부분의 항이 0인 희소행렬의 경우 MEM 낭비 ↑
🤔 행렬의 전치 연산(tranpose)을 구현하는 경우

: 2차원 배열의 요소 (i,j)를 (j,i)로 교환 + 배열을 함수의 매개변수로 전달하고 전달 받음.
( ✨C에서 함수로 배열을 전달하면 항상 원본이 전달됨 <= 배열의 이름이 포인터 역할을 하기 때문)
2) 0이 아닌 요소들만 저장하는 방법
장점: 희소 행렬의 경우 메모리가 절약됨.
단점: 각종 행렬 연산들의 구현이 복잡해짐.
🤔 행렬의 전치 연산(tranpose)을 구현하는 경우
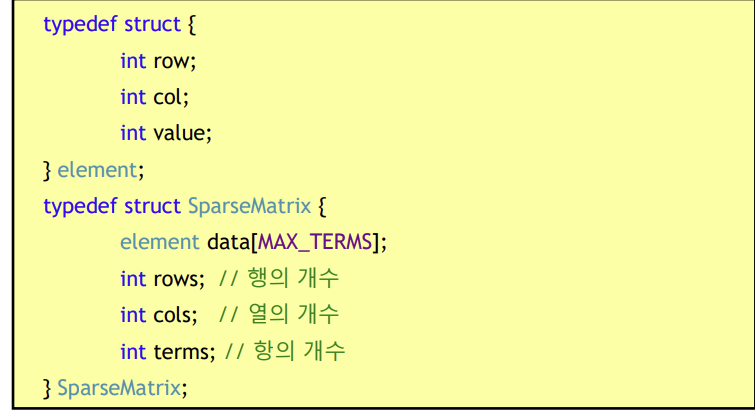
: 행렬에서 하나의 요소는 (row, col, value)로 표현. (구조체로 정의)
-> 기존 행렬의 열이 행으로 변경되기 때문에 0열 처리 -> 1열 처리 -> ... 이렇게 하면 행 순서대로 작성됨.
*처리: 0열에 있는 요소를 모두 찾아서 0행에 저장하는 것.
✨ 낮은 행부터 높은 행까지 오름차순으로 저장되어야 한다는 가정이 필요함.
🃏 포인터
: 다른 변수의 주소를 가지고 있는 변수
* 포인터로 선성된 변수에 저장된 값은 메모리 주소값
🤔포인터 연산자
& : 변수의 주소를 추출하는 연산자
* : 포인터가 가리키는 메모리에 값을 변경하는 연산자
int a = 10;
int *ptr = &a;
printf(" ", &a) = printf(" ", ptr) != printf(" ", &ptr)
=> *ptr과 a는 전적으로 동일하다!
cf) 포인터가 어떤 객체도 가리키고 있지 않을 때는 NULL 포인터 상태로 두는 것이 좋다
🤔 함수 안에서, 매개변수로 전달된 포인터를 이용하여 외부 변수의 값을 변경 가능!

출력 결과
: swap을 호출하기 전: a=1, b=2
swap을 호출한 다음: a=2, b=1
🃏배열과 포인터
* 배열의 이름은 사실상 포인터와 같은 역할을 함.

✨ A = &A[0] = 10 / A+1 = &A[1] = 14 [주소]
*(A+2) = A[2] = 3 [값]

🃏 동적 메모리 할당 (Dynamic memory allocation)
: 프로그램 실행 도중에 메모리를 할당 받는 것 => 필요한 만큼만 할당 받고, 사용 후 반납함.

🤔Heap : OS가 사용하지 않는 메모리 공간을 모아 놓은 것, 동적 메모리가 할당되는 공간
=> Heap 메모리 매니저가 할당해주는 영역이기 때문에 이 영역에는 변수를 선언할 수 없음 (anonymous memory)
** Heap memory는 반드시 pointer로만 사용가능!
🤔포인터 변수의 활용
- 정적으로 할당된 메모리 블록의 값들을 copy&paste로 sub-function에 전달하는 대신, 시작번지만을 매개변수로 전달하고 이를 포인터 변수로 받아서 사용함 => 시공간 절약 가능!
- 런타임때가 되어야 비로소 필요한 메모리 크기를 알 수 있는 경우 (input으로 입력된 값 등), 프로그램 실행 중간에 할당된 stack memory를 포인터로 표기 후 사용하여 유동성을 높일 수 있음!
✔️malloc()
: size 바이트만큼의 메모리 블록을 할당한 후, 이 메모리 블록의 시작 주소(가장 낮은 주소) 를 return
*메모리 블록의 경우, 요청한 크기의 연속된 heap 메모리임.
ex) int *p
p = (int *)malloc(SIZE * sizeof(int));
✔️free()
: 할당된 메모리 블록을 OS에게 반환함.
*반드시 malloc()이 반환한 포인터 값을 기억했다가 반환해야 함.
✨ free( ptr ) 호출뒤에 ptr = NULL 을 넣으면 실수로 ptr을 사용하여 의도치 않는 결과를 초래하는 것을 complier가 막아줌.
🃏 구조체와 포인터
: 포인터를 통하여 구조체의 멤버에 접근하는 편리한 표기법 = ' -> '
*동적으로 생성된 구조체는 포인터를 통해서만 접근할 수 있다. malloc() 함수를 이용하여 구조체를 동적 생성함.

: (*p).name보다 p->name이 더 용이함!
'CSE > 자료구조&알고리즘' 카테고리의 다른 글
| <5> 큐(Queue) (0) | 2023.10.26 |
|---|---|
| <4> 스택(Stack) (0) | 2023.10.26 |
| <2> 순환(Recursion) 과 반복(Iterative) (0) | 2023.10.25 |
| <1> 자료구조와 알고리즘 (0) | 2023.10.24 |
| 선택 정렬(Selection sort)와 삽입 정렬(Insertion sort) (1) | 2023.04.22 |




