밍경송의 E.B
선형 탐색(linear search)과 이진 탐색(binary search) 본문
전형적인 배열에서 특정 값을 검색(원하는 값을 찾을 때까지 왼쪽에서 오른쪽으로 한 번에 한 셀씩 확인)하는 방법을
'선형 탐색'이라고 합니다. 이때! 배열의 정렬 여부가 큰 영향을 미칠 수 있는데요.
정렬되지 않은 배열에서 특정 값(A)을 검색한다고 가정해봅시다. 원하는 값을 찾기 전까지 우리는 모든 원소를 하나도 빠짐 없이 검색해야 합니다.만약 찾으려는 값이 배열에 들어있지 않은 값이라면 배열의 끝에 도달하기 전까지 검색을 멈출 수 없을 것입니다.
한편 정렬된 배열에서는 찾으려는 값이 배열에 들어있지 않을 때도 검색을 더 빨리 멈출 수 있습니다. 찾으려는 값보다 현재 도달한 값이 더 크다면, 그 다음 배열을 검색할 필요가 없으니까요. 예를 들어, 배열 [3, 17, 75,80] 에서 22를 찾는다고 하면 3, 17를 지나 75에 도달했을 때, 22가 없다는 것을 인지하고 그 다음으로 넘어가지 않아도 된다는 말입니다.
$ 정렬된 배열의 선형 탐색 코드 (루비)
def linear_search(array, search_value)
array.each_with_index do |element, index| #배열의 모든 원소를 순회한다.
if element == search_value #원하는 값을 찾으면 그 인덱스를 반환한다.
return index
elsif element > search_value #찾고 있던 값보다 큰 원소에 도달하면 루프를 종료.
break
end
end
#배열에서 값을 찾지 못하면 널을 반환한다.
return nil
endㄴ왜 루비를 썼냐구요.. 저도 루비 잘 몰라요.. 근데 제가 공부하는 책이 루비로 구현하길래 저도 써봤습니다.. 간단하고 괜찮은 거 같아요.. 배울 생각은 없지만 이해하긴 좋은듯! 어렵지 않은 코드니까 주석 참고하시면 될 것 가타요
그렇다면 이진 탐색이란 무엇일까요?
선형 탐색보다 훨씬 빠른! 정렬된 배열에서만 수행할 수 있는 이진 탐색에 대해 알아보겠습니다.
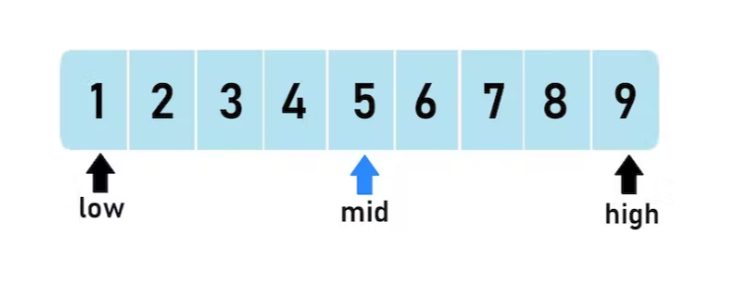
이진 탐색은 정렬된 배열 중 가운데 셀부터 검색을 시작하는데요. 배열의 길이를 2로 나누어 가운데 셀의 인덱스를 계산하여 인덱스에 접근합니다. 가운데 셀을 기준으로 셀을 양쪽으로 나눴을 때, 찾으려는 값이 속해있지 않은 쪽(셀의 절반)은 모두 제거해줍니다. 그럼 셀이 절반이 되었겠죠! 그 상태에서 셀들의 가운데 값을 확인하고, 비교하고, 제거하는 과정을 반복합니다.
*만약, 가운데 값이 2개라면(셀 전체가 짝수인 경우) 임의로 왼쪽 값을 선택합니다.
마지막 남은 셀까지 확인했을 때, 여기에 찾는 값이 없다면 이 (정렬된) 배열에 찾는 값이 없다는 것을 의미합니다.
코드로 함께 이해해봅시다! 자세한 내용은 주석을 참고해주세욥.
def binary_search(array, search_value)
#찾으려는 값이 있을 수 있는 상한선과 하한선을 정한다.
#최초의 상한선은 배열의 첫번쨰 값, 하한선은 마지막 값이다.
lower_bound = 0
upper_bound = array.length -1 #인덱스는 0번째부터 있다요.
#상한선과 하한선 사이의 가운데 값을 계속해서 확인하는 루프를 시작한다.
while lower_bound <= upper_bound do
#상한선과 하한선 사이에 중간 지점을 찾는다.
#짝수라서 딱 떨어지지 않는다면 왼/오 중 한쪽을 택하도록 해야 하지만
#루비의 경우 정수를 나누기할 때 결괏값을 가장 가까운 정수로 '올림'하기 때문에 생략
midpoint = (upper_bound + lower_bound ) /2
#중간 지점의 값을 확인한다.
value_at_midpoint = array[midpoint]
#중간 지점의 값이 찾고 있던 값이면 검색을 끝내고,
#그렇지 않으면 더 클지 작을 지 추측한 바에 따라 상한선과 하한선을 바꾼다.
if search_value == value_at_midpoint
return midpoint
elsif search_value < value_at_midpoint
upper_bound = midpoint -1
elsif search_value > value_at_midpoint
lower_bound = midpoint +1
end
end
#상한선과 하한선이 같아질 때까지 경곗값을 줄였다면 찾고 있는 값이 배열에 없다는 것이다.
return nil
end
**작은 크기의 정렬된 배열이라면, 이진 탐색 알고리즘이 선형 탐색 알고리즘보다 크게 나은 점이 없습니다. 하지만 배열의 크기가 커진다면 어떻게 될까요?
일단 선형 탐색에서는 (최대) 원소 수만큼의 탐색 단계가 필요합니다. 만약, 배열의 원소 수를 두 배로 늘린다면, 검색 단계도 두 배로 늘어나겠죠. 반면 이진 탐색의 경우, 원소 수를 두 배로 늘릴 때마다 검색 단계가 한 단계만 늘어난다는 점이 이해되시나요?
Q. 원소가 100개인 정렬된 배열에서 이진 탐색은 7단계가 걸렸습니다. 만약 원소가 200개인 정렬된 배열이 있다면 이진 탐색은 몇 단계가 걸릴까요?
A. 원소의 수가 2배 늘어났기 때문에, 검색 단계는 1단계 늘어난 8단계입니다!!
'CSE > 자료구조&알고리즘' 카테고리의 다른 글
| <3> 배열, 구조체, 포인터 (0) | 2023.10.25 |
|---|---|
| <2> 순환(Recursion) 과 반복(Iterative) (0) | 2023.10.25 |
| <1> 자료구조와 알고리즘 (0) | 2023.10.24 |
| 선택 정렬(Selection sort)와 삽입 정렬(Insertion sort) (1) | 2023.04.22 |
| 빅 오 표기법 - O(1), O(N), O(log N) (0) | 2023.04.17 |




