밍경송의 E.B
<10> 그래프 1 본문
이 글은 시험이 2일 23시간정도 남은 사람이 내용 정리를 위해 적는 글입니다.
*[C언어로 쉽게 풀어쓴 자료구조] 책과 숙영리 교수님의 강의를 참고하여 작성하였음을 밝힙니다.🐶
🐶그래프
: 연결되어 있는 객체 간의 관계를 표현하는 자료구조 (tree도 그래프의 특수한 경우*뒤에서 다룸)
- G = ( V, E )
- 정점(node, verticle) - V(G) : 그래프G의 정점들의 집합 개수: |V|
- 간선(edge, link) - E(G) : 그래프 G의 간선들의 집합 개수: |E|
⚠️cf 오일러 문제
: 모든 다리를 한번만 건너서 처음 출발했던 장소로 돌아오는 문제
* 다리(edge,link)는 한 번씩만 지나야 함, 육지(node,vertex)는 여러 번 지나도 됨
=> 오일러 정리 : 모든 정점에 연결된 간선의 수가 짝수이면 오일러 경로 존재
*종류
- 무방향 그래프(undirected) - 방향이 없음 (0,1) 과 (1,0) 은 같음. 하나만 쓰면 됨
- 방향 그래프(directed) - 방향이 있음 (0,1) 과 (1,0) 은 다름
- 가중치 그래프(weighted graph) - 간선에 비용과 가중치가 할당된 그래프
- 부분 그래프(sub graph) - 정점 집합과 간선 집합의 부분 집합으로 이루어진 그래프
*용어
- 인접 정점(adjacent vertex) : 하나의 정점에서 간선에 의해 직접 연결된 정점
- 정점의 차수(degree)
- 무방향그래프 : 한 노드에 연결된 모든 선의 수

Q.무방향 그래프에서 모든 노드들의 degree의 합은 ? => 2 x |E|
- 방향그래프
1) 진입차수 : 외부에서 오는 간선의 수
2) 진출차수 : 외부로 향하는 간선의 수

🐶 그래프의 경로
경로 : 노드들의 sequence 혹은 간선들의 sequence
→ 정점 s로부터 정점 e까지의 경로 (s,v1),(v1,v2), ... , (vk, e)
*단순경로(simple path) : 경로 중에 반복되는 노드가 없는 경로
*사이클(cycle) : 단순 경로의 시작 정점 == 종료 정점 (동일)한 경로
*단순 사이클(simple cycle) : (시작점 == 종료점) && (반복노드없음)
Q.오일러 사이클(모든 간선을 한 번만 건너서 처음 장소로 돌아오는 문제)는 simple cycle인가? X
Q.해밀턴 사이클(모든 vertex를 정확히 한 번씩만 방문하여 제자리로 돌아오는 사이클)은 simple cycle인가? O
Ex)

*그래프의 연결 정도
- 연결 그래프(connected=spanning=meshed G) : 무방향 그래프G에 있는 모든 정점 쌍에 대하여 항상 경로 존재

bridge : 없어지면 위 그림과 같이 그래프의 연결이 끊겨 비연결 그래프가 되는 간선을 bridge라고 함.
-완전 그래프(complete G) : 모든 서로 다른 정점이 연결되어 있는 그래프
Q.n개의 정점을 가진 무방향 완전 그래프의 간선의 수는 ? => nx (n-1)/2

🐶 그래프를 구현하는 방법
1) 인접행렬(adjacent matrix) 방법
간선(i,j)가 그래프에 존재 = M[i][j] =1
간선(i,j)가 그래프에 존재 != M[i][j] =0
*무방향 그래프에서 정점i 의 차수 파악하기 (degree) = i번째 행의 값을 모두 더한 값

*방향 그래프에서 정점i 의 차수 파악하기
(out_degree) : i번째 행의 값을 모두 더한 값
(in_degree) : i번째 열의 값을 모두 더한 값

인접행렬의 크기 = |V|^2
인접행렬에서 값이 1인 항의 개수 = (무방향 그래프의 경우) 정점의 차수 = 2 x |E|
인접행렬에서 값이 1인 항의 개수= (방향 그래프의 경우) 간선의 수 = |E|
[구현]
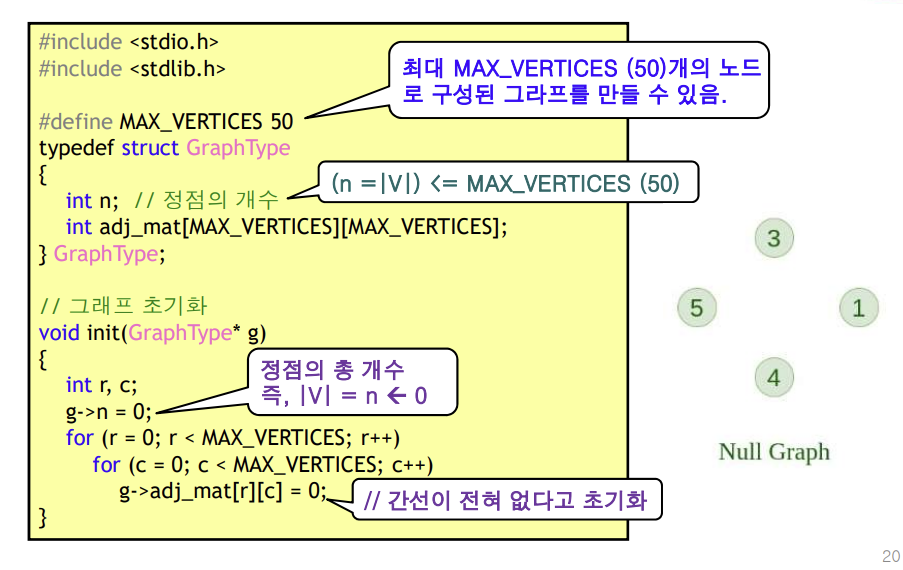

2) 인접리스트(adjacent list) 방법
: 각 정점마다 인접 정점들을 연결리스트(single-linked list)로 표현


*헤더노드 : 크기가 최소 |V| 인 배열(H)로 구현
*인접리스트에서 총 노드(data +link)의 개수는 위의 인접행렬에서 값이 1인 항의 개수와 같음.
🐈 그래프 탐색
" 하나의 정점(source node)으로부터 시작하여 차례대로(order) 모든 정점들을 한 번씩(target node까지) 방문해라 "
[알고리즘]

1) 깊이 우선 탐색(DFS) - 스택 이용
: 한 방향(source에서 멀어지는 방향)으로 갈 수 있을 때까지 가다가 -> 더 못 가면 가장 가까운 갈림길로 돌아와서 다른 방향으로 다시 탐색하는 방법 (중간 범위 중에 배운 미로탐색 문제 같다!>.,,)

Ex)
아래와 같은 그래프를 DFS 알고리즘을 이용하여 탐색할 때, 각 시점마다 stack의 상태와 output을 쓰시오!


=> 위의 예제같은 경우 Q> stack의 최대 높이 2겠죵.
*stack에서 pop되는 시점은 언제일까?
=> 더 이상 순환호출할 인접노드가 없는 경우!
*이미 방문한 노드는 스택에 push하지 않음 ! = 방문하지 않은 인접노드의 경우에만 push!
🐈DFS- tree : DFS 중 방문된 노드를 순서대로 연결하면 트리가 된닥

Q. G에 cycle이 있는지 검사하는 알고리즘
: DFS-tree의 임의 노드에서 ancestor로의 간선이 있으면 cycle 존재
: G에 DFS-tree에 포함되지 않는 edge가 있으면 cycle 존재
⚠️ 여기가 혼란이 .. 있었는데 허허 일단 정리를 해보자면,
트리는 일종의 그래프잔하욥 근데 이제 |E| = |V| -1인 구조를 갖는 그래프 그러니까 트리구조 != 트리임. 트리는 내가 생각하는,, 루트에 따라 달라지는 거지만, 트리 구조는 시작정점을 뭘로 하느냐에 따라 달라지는 게 아닌가바여 구조 그 자체니까..
그래서? 시작 정점을 뭘로 잡느냐와 상관 없이 동일한 '트리 구조'다 이말!!!
Tree 구조인 그래프 G의 DFS-tree는 그래프 G 자체임 == DFS-tree에 포함되지 않는 간선은 없음
== cycle이 존재하지 않음 == 그래프에 loop를 포함하지 않음 == G의 DFS-tree는 unique함
cycle(loop)가 존재하는 그래프 G== DFS-tree에 포함되지 않는 간선이 있음 == G의 DFS-tree는 unique하지 않음
(방문순서에 따라 tree가 달라질 수 있어서! -> 이 말은 간선 자체가 달라지는 거임)
[코드]
*인접행렬

g->adj_mat[v][w] && !visited[w] : 값이 1인 애들(간선이 존재하는) 중에 아직 방문하지 않은 정점 w에서 새로 시작
*인접리스트

!visited[w->vertex] : 아직 방문하지 않은지만 확인
-> 인접리스트의 경우 인접정점들 (간선이 있는 애들)이 이미 표현되어 있기 때문에 간선 존재 확인 여부 불필요
2) 너비 우선 탐색 (BFS) - 큐 이용
: 시작 정점으로부터 가까운 정점을 먼저 방문하고, 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법
-> 시작정점에서 가까운 노드들을 큐에 넣고, 먼저 들어간 순서대로 꺼냄

DFS는 한 방향으로 진행해서 인접정점 중 하나만 먼저 넣고 하는데, 얘는 그 정점의 인접정점을 다 넣어버리구 넘어가는 것이여
[코드]
*인접행렬

*인접리스트

'CSE > 자료구조&알고리즘' 카테고리의 다른 글
| <12> 정렬 (0) | 2023.12.14 |
|---|---|
| <11> 그래프2 (0) | 2023.12.14 |
| <7> 원형 연결리스트, 이중 연결리스트 (1) | 2023.10.26 |
| <6> 단일 연결리스트 (1) | 2023.10.26 |
| <5> 큐(Queue) (0) | 2023.10.26 |




