밍경송의 E.B
<11> 그래프2 본문
이 글은 시험이 1일 어쩌고정도 남은 사람이 내용 정리를 위해 적는 글입니다.
*[C언어로 쉽게 풀어쓴 자료구조] 책과 숙영리 교수님의 강의를 참고하여 작성하였음을 밝힙니다.🦭
신장트리
: 그래프 내의 모든 정점을 포함하는 트리 (|V|-1개의 |E|를 가짐)

🦭 MST(최소비용신장트리) 🦭
: 그래프의 모든 정점들을 가장 적은 수의 간선과 비용(가중치 그래프의 경우) 으로 연결 -> 전체적으로 비용 감소 목적
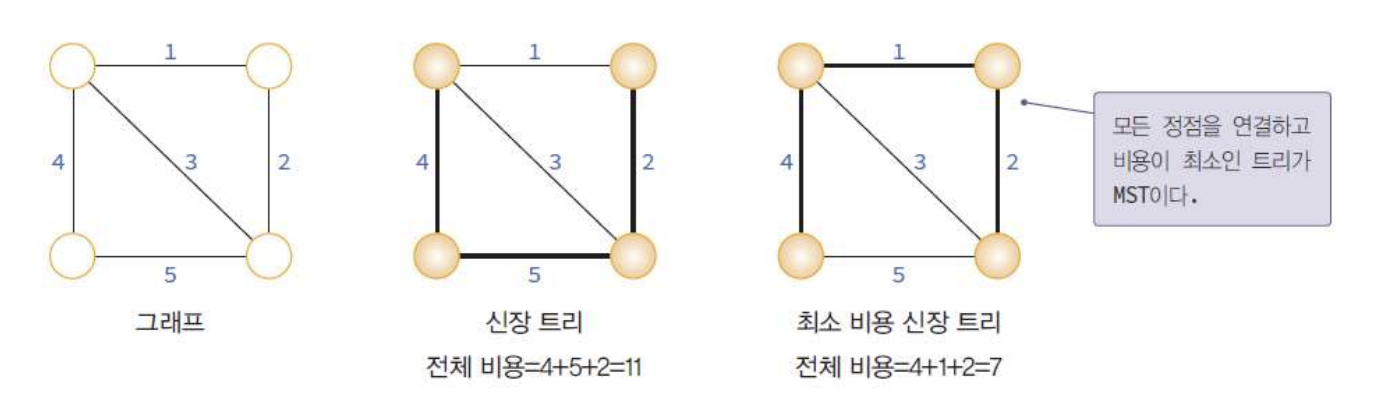
*if weight가 동일한 간선이 있다면, 여러 MST가 나올 수도 있음!
그래프 G = (V,E)의 MST G' = (V',E')의 조건
1) V = V'
2) E'은 E의 부분 집합, |E'| = |V| -1 (no cycle in G')
3) Sum(weight of edges in E') is minimum
그래 MST도 트리지 그래 그러면 cycle이 없겠구나 그래그래
🦭1 Kruskal's MST 알고리즘

*ecounter : 현재 MST에 포함된 edge의 개수 (가 node -1 개가 될 때까지 while문을 돌아라)
*k : 현재 (weight이 작은 순서부터) 검사한 edge의 수
Ex)
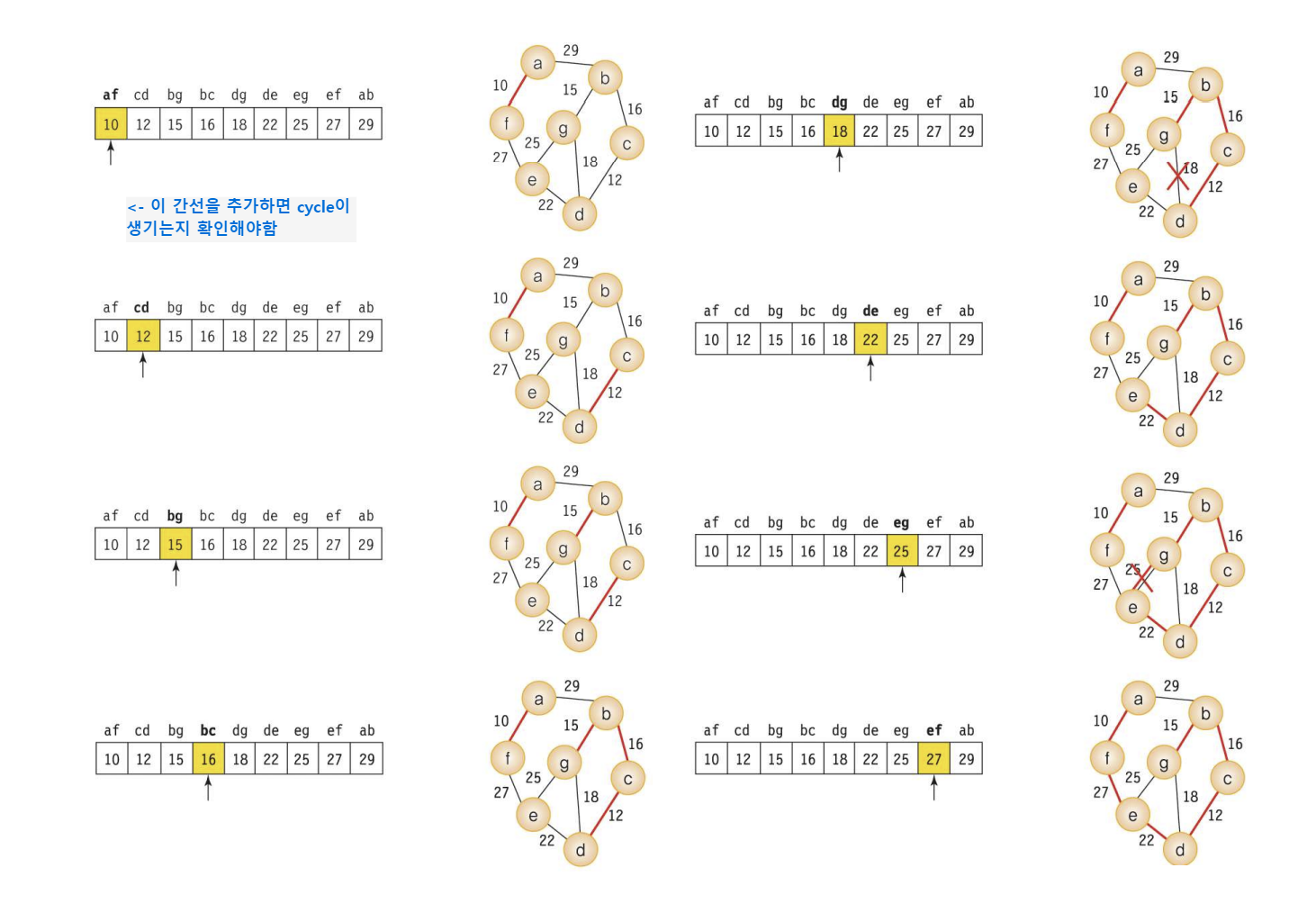
=> {ek}를 추가하면 cycle이 생기지 않는다는 것을 어떻게 확인할 수 있을까?
"UNION-FIND 연산=Disjoint-set algorithm"
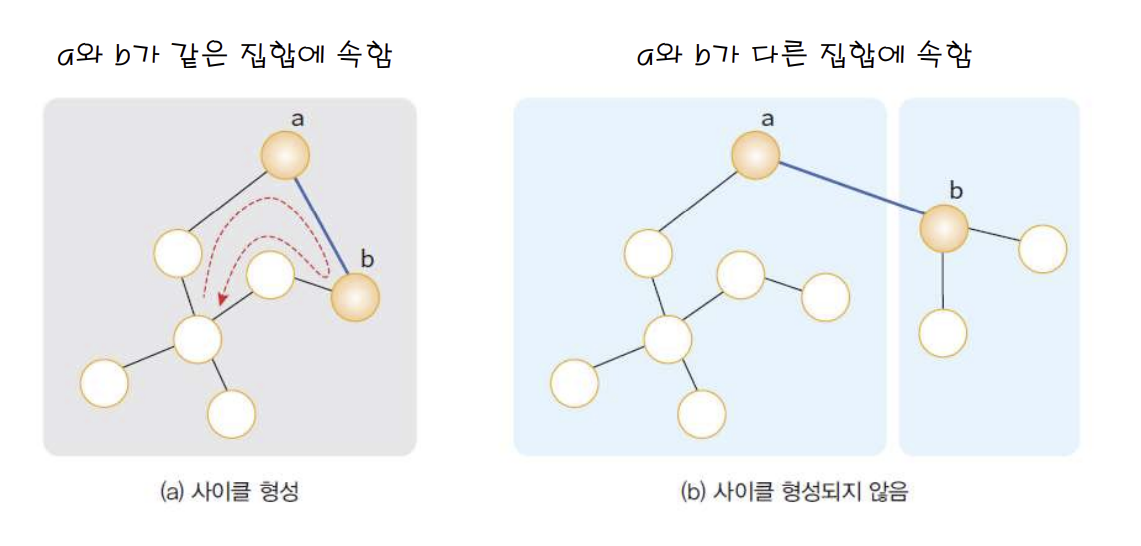
[알고리즘]
내가 연결하려는 두 노드가 같은 집합에 있는지 확인하고, 없으면 연결하는 !

⚠️ 4번째 줄에 parent[root1] = root2;
: 노드 a의 루트인 노드의 부모를 노드 b의 루트 노드로 하겠다 !
그러니까 만약 null graph 상태라면 b→a 요렇게 연결되는 거임 순서에 주의하쟈
UNION(a,b) = b→a .. 이렇게 됩니다
그렇다보니 UNION(b,a)랑 (a,b)는 다르겠
UNION-FIND (X,Y) 연산 잘하는 법 - 만약 연산이 줄줄이 나올 때라면!
1) X의 루트를 찾자 (-1인지 다른 노드 값인지 암튼 찾자)
2) Y의 루트를 찾자
3) 같지 않다면 P[1)] =2) 노드 연결하기 (간선 생성)
4) 1)의 값을 2)의 값으로 바꿔주기
처음 풀 때 헷갈렸던 거는.. null, UNION(H,C) , UNION(H,G) 요렇게 순차적으로 나올 때
첫 번째 연사에 의해서 C→H 이렇게 연결되고, 뒤에 연산을 할 때는 P[C] = G 니까 G →C→H 요렇게 되는 거를 이해 못 해따!
Q. X와 Y의 대표(루트)노드가 같은가 ? = ((FIND(X)==(FIND(Y))? = X와 Y가 같은 그룹에 속했는가? = X와 Y 사이에 간선을 추가하면 cycle이 생기는가?
U-F를 이용한 kruskal 프로그램
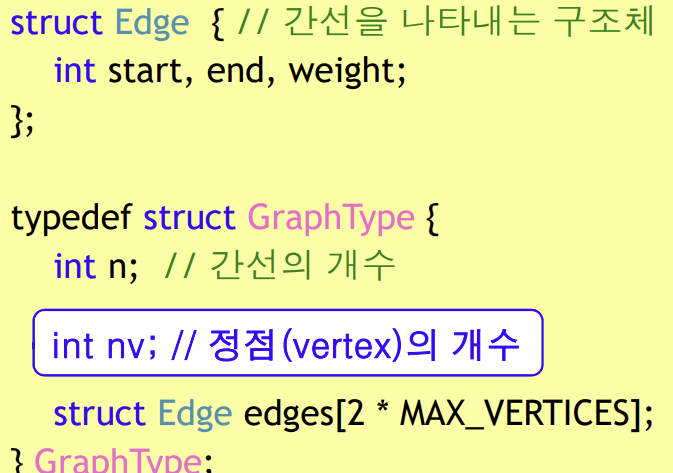

🦭2 Prim's MST 알고리즘
: 시작 정점(아무 노드나)부터 출발하여 신장트리 집합을 단계적으로 확장 - 신장트리 집합에 인접한 정점 중에서 최저 간선으로 연결된 정점을 선택하여 집합에 추가
*Kruskal은 weight이 적은 간선부터 골랐는데 얘는 시작노드를 중심으로 퍼져나가는 느낌스
Ex)
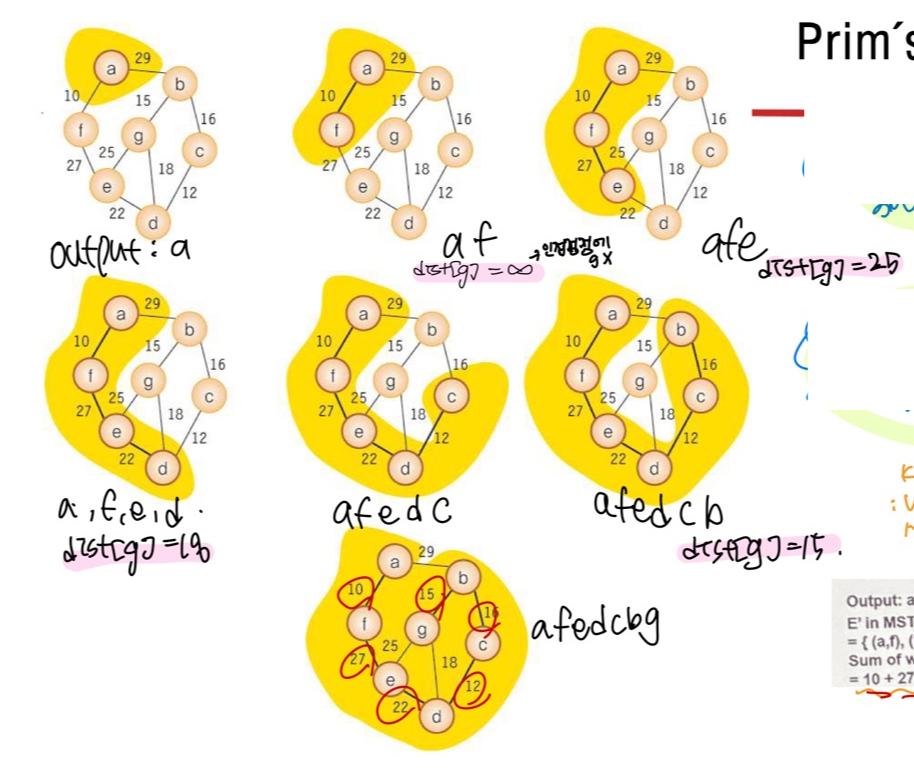
Q. 노드 b부터 시작할 때 3번째로 추가되는 간선의 w는?
Q. g의 dist가 몇 번이나 업데이트 되는가?
[알고리즘]

*dist[v]: v가 현 MST와 직접 연결된 간선의 weight
*시작정점이 무엇인지에 따라 MST 집합에 간선이 추가되는 순서는 달라질 수 있지만, 최종적으로 얻어지는 MST의 구조는 달라지지 않는다악!
=> Uniqueness of MST
: G의 모든 간선의 weight이 다르다면, MST는 unique하다.

* if (!selected[v] && g->weight[u][v] < distance[v])
: 아직 MST에 포함되지 않은 노드이면서, 이전 MST와의 거리(dist[v])보다 직전에 MST에 포함된 노드(u)를 통한 간선의 거리(g->weight[u][v])가 더 가깝다면! distance[v]를 업데이트해라~~
*Prim은 시작정점과 연결된 그래프 안에서만 작동!!!!
ㄴ 생각해보면 Kruskal은 그냥 w에 따라 진행해나가는 거니까, disconnected 된 그래프여도 동작 가능한데, 얘는 인접정점 기준으로 뻗어나가니까 ...융 그럴 수 있네
주어진 G의 weight이 모두 distinct라면 Kruskal로 얻은 결과나 Prim으로 얻은 결과나 동일함!
(순서는 다를 수도 같을 수도 있음엽)

정리🤔

Prim에서 하나의 노드를 여러 번 방문한다는 소리는 dist[x]를 계속 계속 업데이트한다는 그런 뜻!
그래서 희박한 그래프는 kruskal이 굳, 밀집된 그래프는 prim이 굳이랍니다!
.. 왤케 많쥐..
🐈 Shortest Path (최단경로) 🐈
: 경로란.. 시작정점과 종료정점이 제시된 것.
최단 경로란? 정점u와 정점 v를 연결하는 경로 중에 간선들의 가중치 합이 최소! 가 되는 경로
*MST랑 관점이 아예 다름..이 포인트
⚠️가중치 인접행렬을 갱신해가며 사용함. *직접가는 간선이 없는 경우 : 무한으로 표
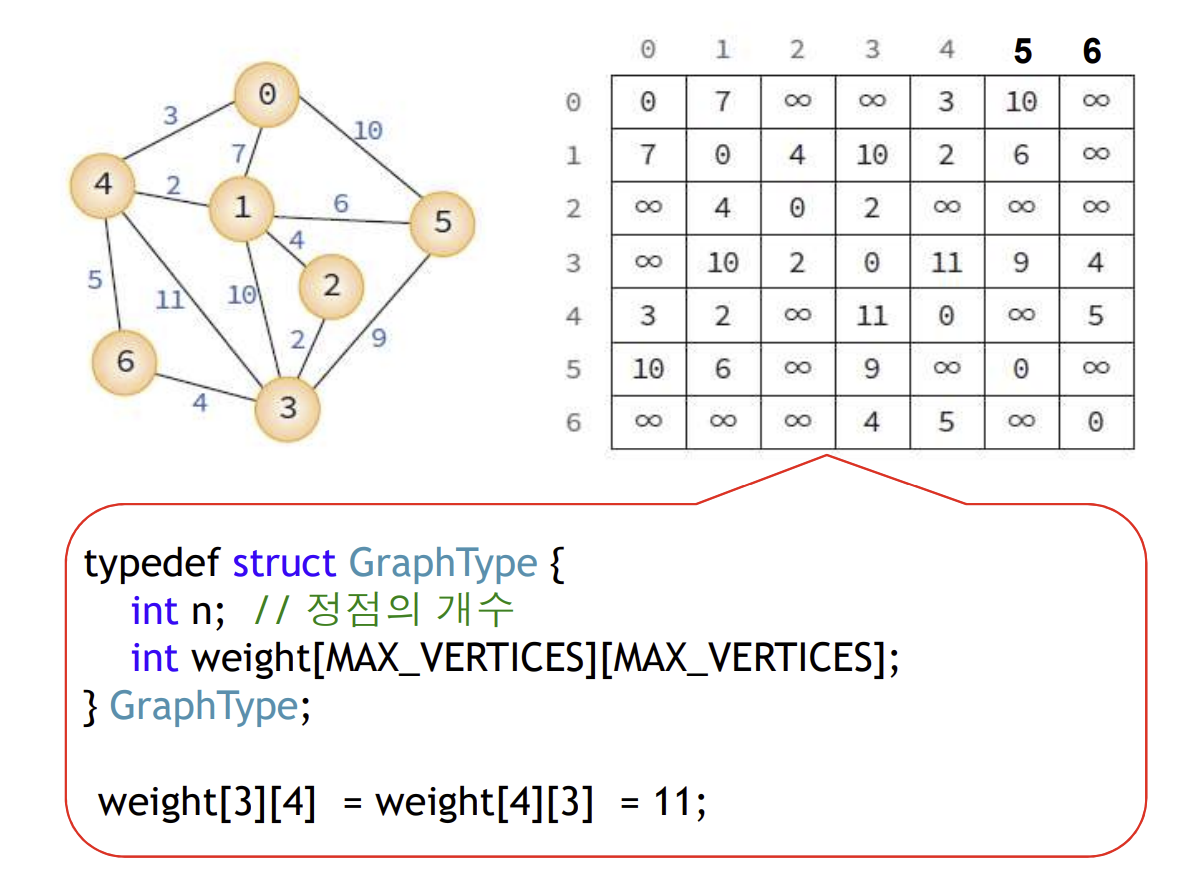
🐈 Dijkstra 알고리즘🐈
: 하나의 시작 정점(기준)에서 다른 모든 정점(|V|-1) 까지의 최단 경로를 계산하는 알고리즘
*집합 S: 시작 정점으로부터 최단 경로가 이미 발견된 정점들의 집합
한 노드가 S에 들어갔다? = 시작 정점으로부터 그 노드까지의 최단 경로가 밝혀졌다! (추리게임같네....
*distance[] : 최단 경로가 알려진 정점들만 이용한 다른 정점들까지의 최다 경로 길이. (계속 바뀜 주의)
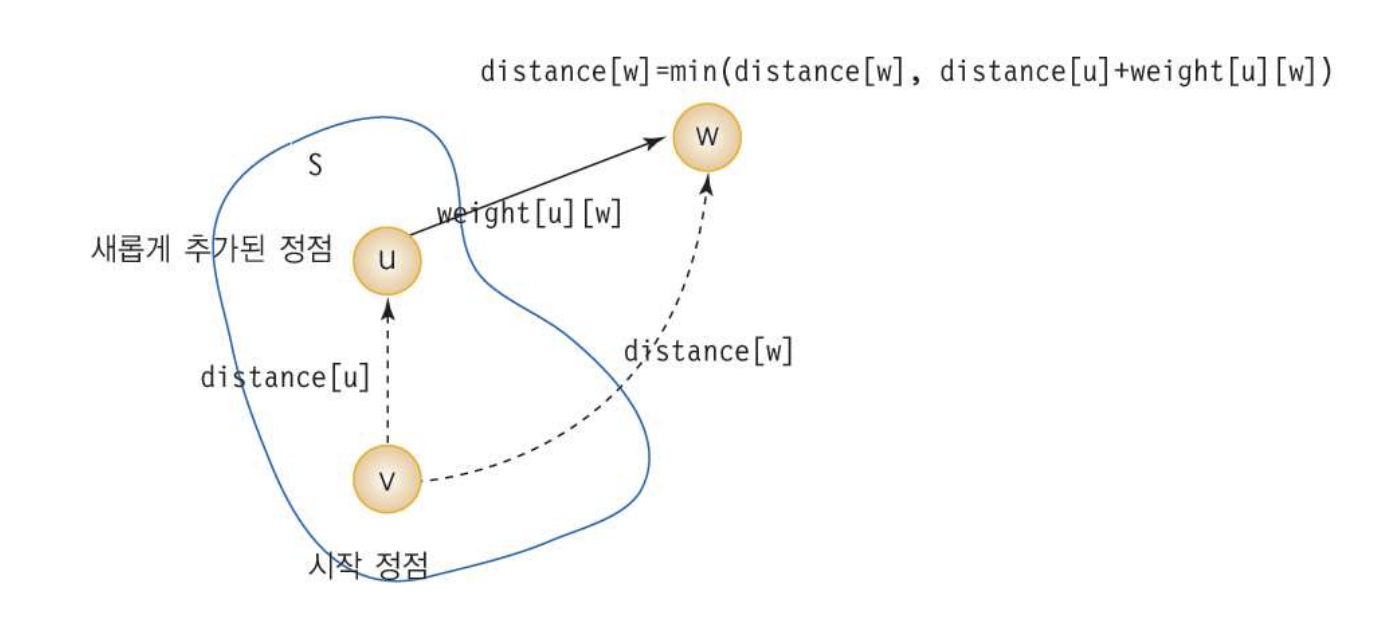
⚠️ round를 한 번 돌 때마다, 하나의 정점으로의 shortest path가 구해짐
증명은 그림으로 대체...
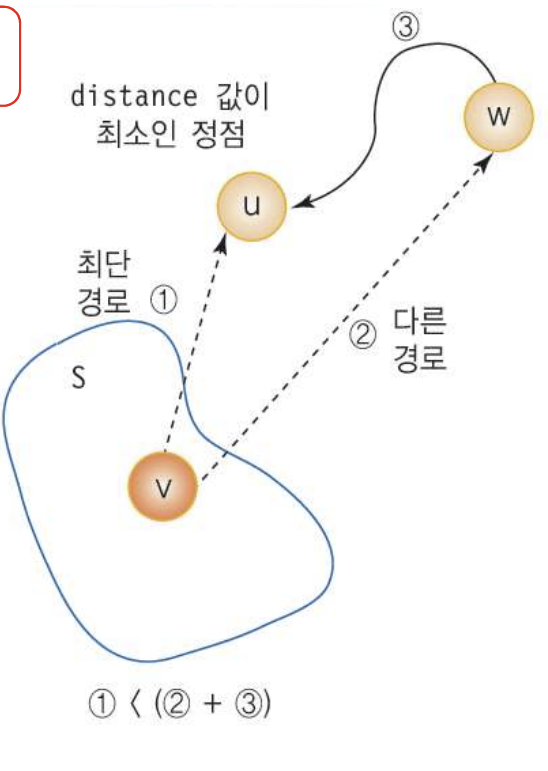
*여기서 중요한 것은 이 증명이 성립하려면 간선의 가중치는 0보다 작으면 안된다는 것!
그럼 합이 최단 경로보다 작아질 수도 있기 때문에... ! 0까지는 가능함
[알고리즘]

EX)
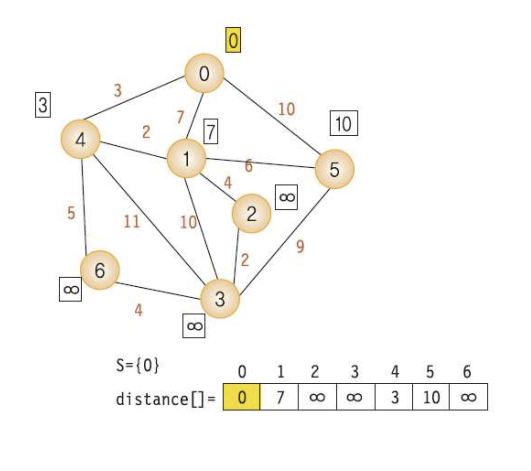

⚠️헷갈렸던 거는.. s= {0,4,1}일 때, s 자체를 한 뭉텅이?로 보고 음 거기서 제일 짧은 간선은 2로 가는 거니까 2인가보다~ 했는데 이거는 Prim 알고리즘이었던 것.. ㅠ 몬가 시작 정점이 있다는 거 땜에 둘이 잠깐 헷갈림
그러니까,, Dijkstra 이거는 s에 없으면서, 그때 그때 시작정점으로부터 제일 가까운 애를 고르는 것임!
그림에서 2번째 표에서 6이 가중치 8로, 선택되지 않은 애들 중에 제일 가까운 애니까 걔를 골라야!>.! 했다
표를 무족건 그리자 무조건 잘.
[알고리즘]

min-heap을 사용하면 O(|V| *log|V|) 안에 해결이 가능하다....고 한다.
🐈 Floyd 알고리즘🐈
: 모든 정점에서 다른 모든 정점까지의 최단 경로를 계산하는 알고리즘
[알고리즘]

* 음의 가중치를 허용
다른 내용은 오히려 이해를 어렵게 만드는...데 요걸 보면 좀 이해가 간다
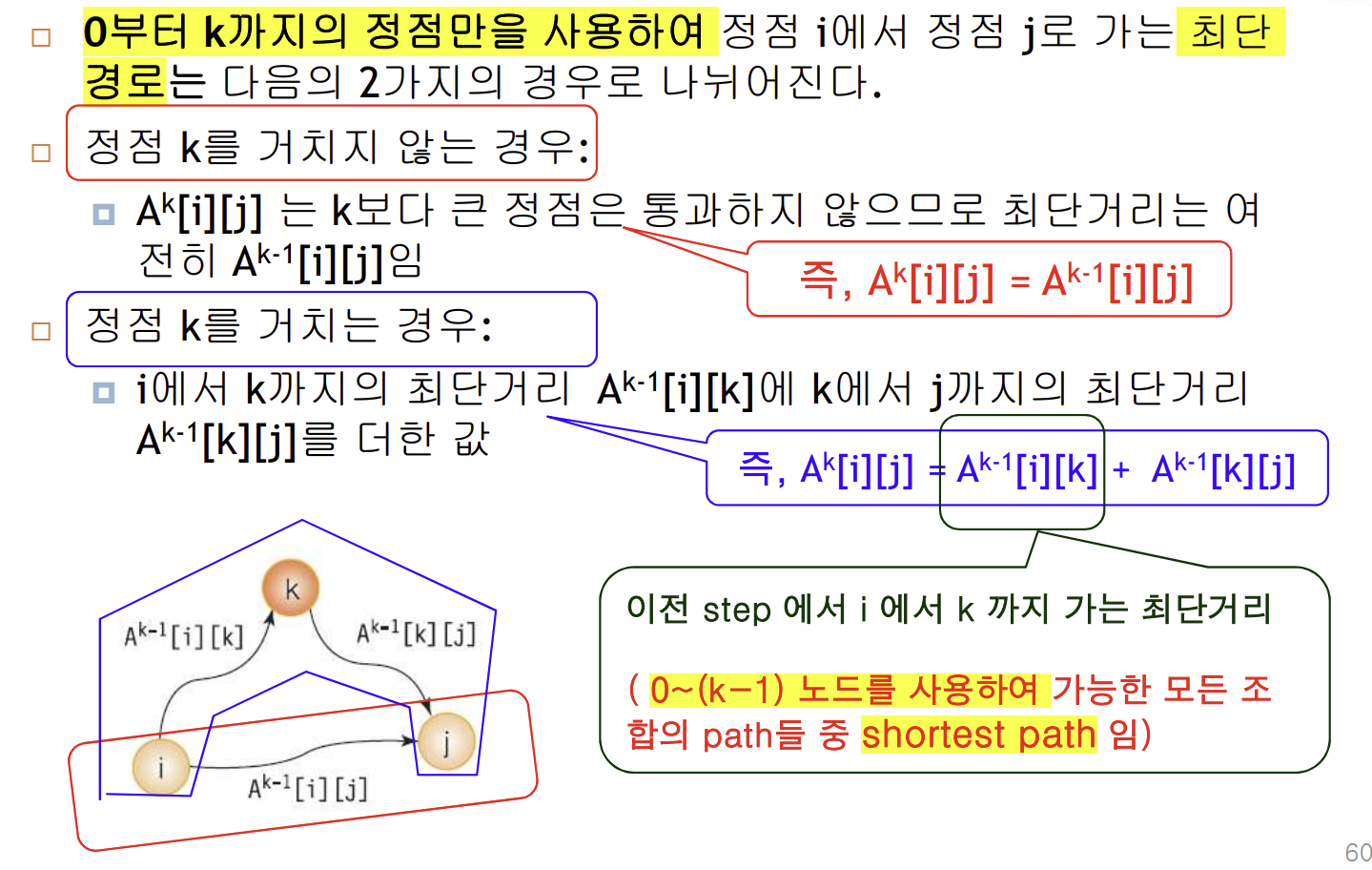
EX)
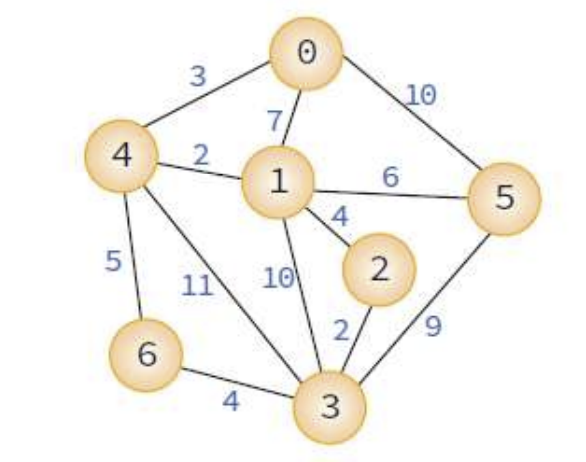

: A^0[i][j] = min(A^-1[i][j], A^-1[i][0] + A^-1[0][j])

: A^1[i][j] = min(A^0[i][j], A^0[i][1] + A^0[1][j])
이거를 모든 정점에 대해서 다 해보면 완-성! 안 하고 싶다...
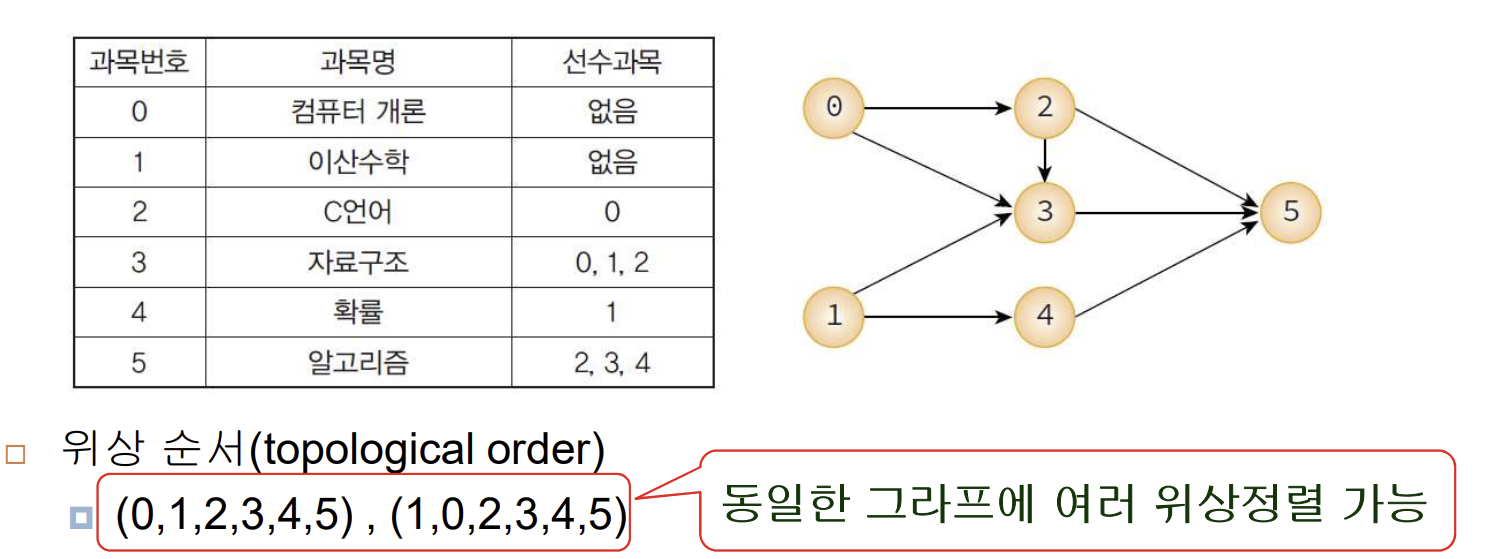
🐲위상정렬(topological) 🐲
: 방향 그래프이면서 사이클이 없는 G에서, 정점들의 선행순서를 위배하지 않으면서 모든 정점을 나열
⚠️ 여기서 알아야할 것은 선행 노드가 존재한다 = 그 정점으로의 in_degree 값이 존재한다
-> 따라서? 시작 정점을 in-degree가 0인 노드로 하는 것이 좋다!
[알고리즘]

[EX]
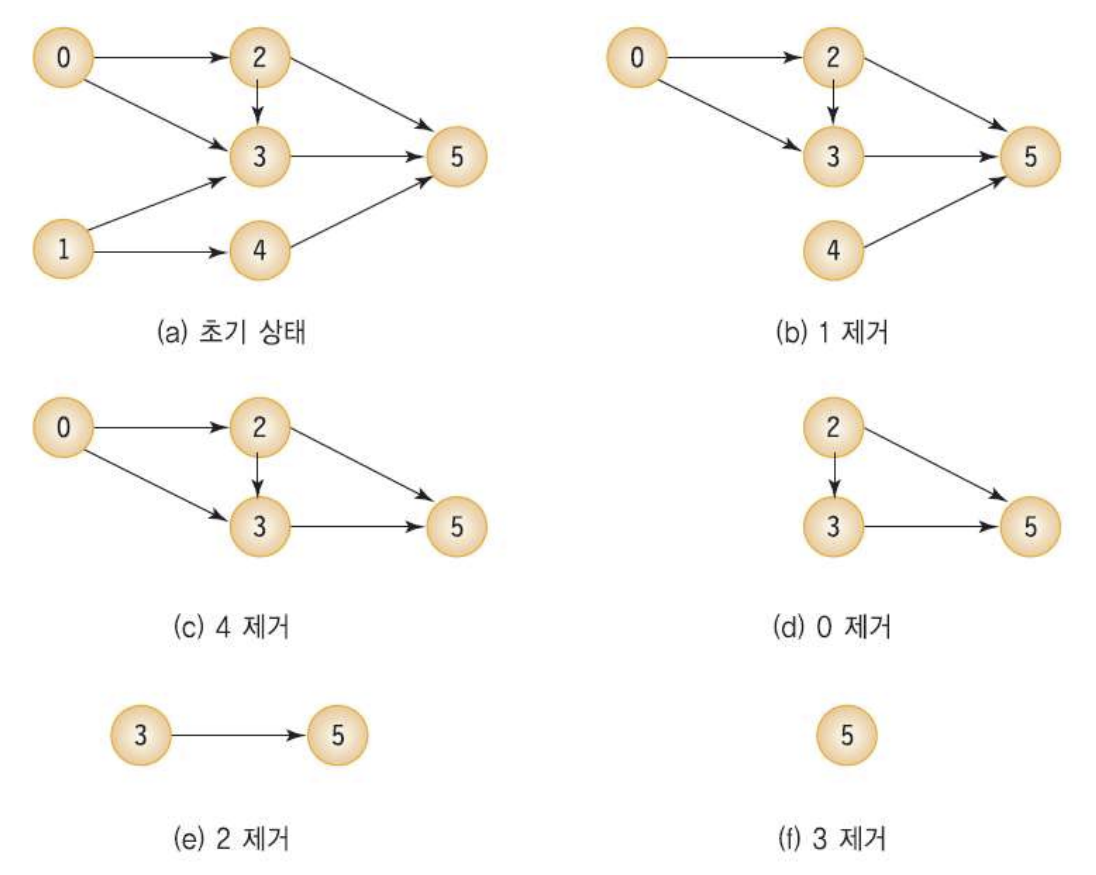
*코드에서는 스택을 이용했는데, 큐를 이용해도 된다고 합용


*위의 예제대로 보면, 일단 in_degree가 0인 정점이 1이랑 0이니까 얘네가 스택에 들어가겠조 (요 순서는 아마 정해야할듯)
그 다음에 1이 pop되고, 1이 pop됨으로써 in_degree가 0이 되는 정점을 push해주고 또 pop하고 요런 식으로 하는 것!
stack의 상태 변화나 pop되는 순서 같은 거 물어보기 굳.>!!!!!!!
끝.
'CSE > 자료구조&알고리즘' 카테고리의 다른 글
| <12> 정렬 (0) | 2023.12.14 |
|---|---|
| <10> 그래프 1 (0) | 2023.12.12 |
| <7> 원형 연결리스트, 이중 연결리스트 (1) | 2023.10.26 |
| <6> 단일 연결리스트 (1) | 2023.10.26 |
| <5> 큐(Queue) (0) | 2023.10.26 |




